Il test delle ipotesi

Nella vita di tutti i giorni, dobbiamo spesso prendere decisioni basate su informazioni incomplete.

Può darsi ad esempio che si debba decidere se una certa procedura educativa sia più efficace di un’altra, se un nuovo farmaco abbia risultati realmente positivi sull’evoluzione di una malattia, e via dicendo.

Il test delle ipotesi è una procedura statistica che ci consente di porre un quesito sulla base di informazioni campionarie, al fine di raggiungere una decisione statisticamente significativa.

In termini più chiari e diretti: la mia scoperta sperimentale è dovuta al caso?
Il test delle ipotesi è proprio una procedura statistica per verificare se il caso sia una spiegazione plausibile di un risultato sperimentale.

Una premessa…

---

Bisogna capire la differenza tra probabilità e inferenza.

• Se conosco i dati della popolazione e voglio sapere qual è la probabilità di avere un dato risultato, ci troviamo nel campo della probabilità.
  
• Se da un campione cerco di inferire i valori della popolazione, siamo nei territori dell’inferenza.

Ipotesi statistiche

Nel test delle ipotesi abbiamo sempre da “soppesare” due ipotesi. Lo status quo è chiamato ipotesi nulla ed ha simbolo H₀

Quello che faremo è di andare a testare l’ipotesi nulla contro un’ipotesi alternativa, a cui diamo il simbolo H_a

N.B. In genere, l’ipotesi alternativa è quella a cui crediamo!

Scegliamo poi un livello di significatività o alpha level α.
Lo standard comune è α = 0.05, cioè un livello di significatività al 95%.
In base all’alpha level possiamo stabilire la o le regioni critiche.

Se il valore che otteniamo con il nostro test cade in una regione critica, respingeremo l’ipotesi nulla, accogliendo l’ipotesi alternativa.

Un semplice esempio grafico di rappresentazione. Ipotizzo un test in cui stabilisco l’ipotesi alternativa che la media risulti maggiore della media dell’ipotesi nulla. Si tratta di un caso in cui ho una sola zona critica, in questo caso quella a destra del valore α. Per rigettare l’ipotesi nulla il valore del mio test dovrà cadere nell’area grigia:

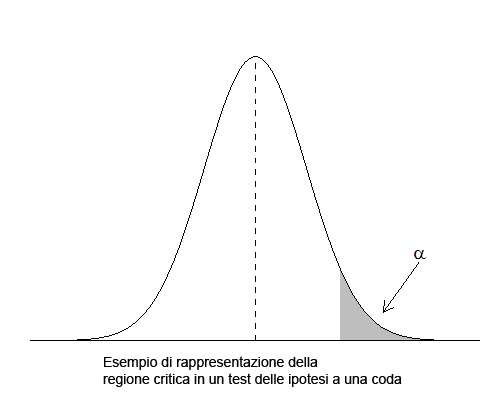
Errori di I e II tipo

Il risultato raggiunto, ovviamente, non costituisce una certezza.

Il livello di significatività del test (nel nostro primo esempio il 95%) ci indica la probabilità di incorrere in un errore di I tipo, cioè di rifiutare erroneamente l’ipotesi nulla, che era vera, accettando l’ipotesi alternativa.

Come si vede, possiamo determinare il livello di significatività del nostro test, cioè possiamo fissare la probabilità massima con cui accettiamo di rischiare l’errore di I tipo.

Se invece accettiamo come valida l’ipotesi nulla, quando doveva essere rifiutata in quanto falsa, compiamo un errore di II tipo.

Il modo più chiaro che ho trovato per spiegare il concetto è questo…

Il calcolo della probabilità di incorrere in un errore di tipo II non è così diretto come nel caso dell’errore di tipo I, e lo affronterò in maniera un po’ semplificata più avanti.

Una o due code? Questo è il problema…

Il test può essere a 1 coda, ad esempio se l’ipotesi alternativa è che una media sia maggiore della media che rappresenta l’ipotesi nulla:

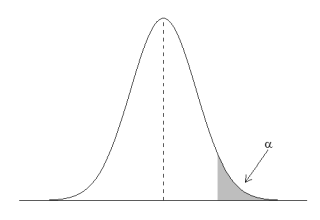
oppure a 2 code (se l’ipotesi alternativa è che la media che ipotizzo sia diversa dall’ipotesi nulla).

Nell’ipotesi a 2 code avremo 2 regioni critiche ai due estremi della curva, ciascuna delle quali rappresenta un livello α/2:

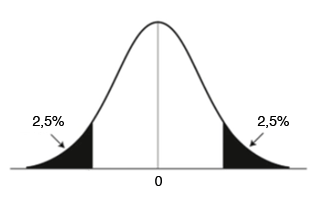
Riassumiamo per punti

1. Stabilisco l’ipotesi nulla e l’ipotesi alternativa.
2. Fisso il livello di significatività (alpha level).
3. Quale distribuzione usare: normale o t?
4. Raccolgo e analizzo i dati.
5. Traggo le conclusioni.

Devo pormi una domanda fondamentale: ma quale distribuzione devo utilizzare?

La risposta può essere trovata guardando al sigma (la deviazione standard o scarto quadratico medio) e la numerosità del campione. Mi chiedo:

Conosco il sigma della popolazione? (nella realtà un caso abbastanza raro…). Ho un campione sufficientemente numeroso (n>30) ?

Se la risposta è SI, allora uso la distribuzione normale (e calcolo lo Z-score).

Se la risposta è NO, cioè se non conosco il valore del sigma della popolazione (o se sto lavorando con campioni numericamente esigui), allora userò la distribuzione t o distribuzione di Student.

n.b. quando il campione diventa numeroso, la distribuzione t approssima sempre di più la normale…

C’è bisogno di un esempio

Voglio condurre un test delle ipotesi in una situazione nella quale conosco il sigma della popolazione.

Seguiamo i nostri passaggi.

1 – Stabilisco l’ipotesi nulla e l’ipotesi alternativa

Se:

\( H_{0}: \mu = x \\ H_{a}: \mu \neq X \\ \)

allora siamo di fronte a un test a 2 code. Avremo cioè due zone critiche da considerare.

Se invece:

\( H_{0}: \mu = x \\ H_{a}: \mu > X \\ \)

allora il test è a una coda.

2 – Fisso il livello di significatività (alpha level)

Scegliamo il caso più tipico, un livello di significatività pari al 95%, quindi:

\( \alpha = 0,05 \)

3 e 4 – Scelgo la distribuzione e Raccolgo e analizzo i dati

Suppongo di avere raccolgo i dati. Mi chiedo ora quale tipo di distribuzione devo usare per il mio test. La domanda è sempre quella:

Conosco il sigma della popolazione?

Nel mio esempio diciamo di sì, e allora usiamo la normale…

Calcoliamo lo Z-score. Trovo:

\( \sigma_{\bar{x}}= \frac{\sigma}{\sqrt{n}} \\ \)

ora posso trovare Z:

\( Z = \frac{\bar{x} – \mu}{\sigma_{\bar{x}}} \\ \)

5 – (finalmente) Traggo le conclusioni

Mettiamo che il test sia con :

\( H_{0}: \mu = x \\ H_{a}: \mu \neq X \\ \)

quindi a 2 code. Il livello di significatività prescelto è il 95%, dunque vado a cercare 2,5% (5%/2) sulla tavola, e trovo il valore 1.96.

n.b. avrei potuto usare R con la funzione: 

qnorm(0.025)

Se invece non ho la tabella a portata di mano e non voglio scomodare R, posso trovare al volo il valore con la fidata calcolatrice Casio:

Shift CATALOG
InvNormCD(0.975)

Se uso una gloriosa TI-83 potrò ottenere il valore facilmente così:

2nd DISTR
3 (invNorm)
invNorm(0,975)

Qualunque strumento io abbia utilizzato, il valore che troverò sarà di (arrotondando) 1.96.

Quindi -1,96 e +1.96 sono i valori critici.

Se il mio Z-score risulta, per esempio, di 2.50, noto immediatamente che il valore risulta compreso nella zona critica. Allora posso rigettare l’ipotesi nulla e accettare quella alternativa.

Due consigli al volo:
1) Disegniamo sempre il grafico. Ci aiuterà moltissimo a non commettere errori.
2) I livelli di significatività più comunemente usati sono quelli al 5% e all’1%. I valori critici nel caso di test a una coda oppure a due code che più spesso troveremo e che quindi possiamo imparare sono:

livello significatività	una coda	due code
5% (alpha 0,05)	1.65 (+ oppure -)	+/- 1.96
1% (alpha 0,01)	2.33 (+ oppure -)	+/- 2.58

Semplificarsi la vita: scrivo una funzione in R

Mi semplifico la vita e mi preparo una funzione in R, che chiamerò z-test:

z.test = function (x,mu,popvar) {
  one.tail.p <- NULL
  z.score <- round((mean(x)-mu)/(popvar/sqrt(length(x))),3)
  one.tail.p <- round(pnorm(abs(z.score),lower.tail=FALSE),3)
  cat("z=",z.score,"\n","one-tailed probability =",one.tail.p,"\n","two- tailed probability =",2*one.tail.p)
}

Se sto Usando una TI-83:

Con la TI-83 scelgo:

STAT   poi
TESTS   quindi
Z-TEST   a seguire
STATS

\( \mu_{0} = media \\ \sigma = sigma \\ \bar{x} = media\ del \ mio \ campione \\ n = numero \ campioni \\ \mu \neq \mu_{0} \ se\ il\ mio\ test\ è\ a\ due\ code \\ \\ CALCULATE \\ \)

Con la casio

MENU / STAT
F3 TEST
F1 Z
F1 1-s

inserisco i dati e poi scelgo

CALC

La probabilità di un errore della seconda specie

Come abbiamo visto, la probabilità di incorrere in un errore della prima specie è fissato a priori nel nostro test scegliendo il livello di significatività, l’alpha.

Ipotizziamo, ad esempio, che una certa rilevazione relativa a un valore ipotizzato della media abbia come ipotesi nulla un valore pari o superiore a 260.
La mia ipotesi alternativa è dunque che questo valore medio sia minore di 260.
Stabilisco poi che un valore di 240 0 meno costituirebbe uno scostamento importante.
Nel mio esempio, il livello di significatività è fissato al 95% (alpha=0.05), il campione consta di 36 osservazioni, lo scostamento medio è di 43.

\( \bar{X}_{critico}=\mu_0 + z\sigma_{\bar{x}}=\\ 260+(-1.65)(7.17)=248.17\\ \)

dove

\( \sigma_{\bar{x}}=\frac{\sigma}{\sqrt{n}}=\frac{43}{\sqrt{36}}=\frac{43}{6}=7.17\\ \\ \)

Come abbiamo più volte ripetuto la probabilità dell’errore di 1 specie è uguale al livello di significatività, dunque 0.05 (il 5%).

La probabilità di errore della seconda specie è la probabilità che la media del campione casuale sia >= 248.17.

Se faccio la mia rilevazione e trovo una media di 240:

\( z=\frac{\bar{X}_{critico}-\sigma_1}{\sigma_{\bar{x}}}=\\ \frac{248.17-240}{7.17}=\frac{8.17}{7.17}=1.14\\ \\ \)

Quindi:

P(errore seconda specie) = P(z>=1.14)= 0.1271
cioè circa 0.13, il 13%.

Se mantengo costante il livello di significatività e la dimensione del campione, ma fisso lo specifico valore alternativo della media in modo da allontanarlo dal valore fissato nell’ipotesi nulla, allora la probabilità di errore del 2°tipo diminuisce; al contrario, il valore di tale probabilità aumenterà qualora il valore alternativo venisse fissato in modo da avvicinarsi a quello dell’ipotesi nulla.

Potenza? Ma non era una città?

Nel test delle ipotesi la nozione di potenza si riferisce alla probabilità di rifiutare una ipotesi nulla, dato uno specifico valore alternativo del parametro (nel nostro esempio, la media della popolazione).

Indicando con β la probabilità di errore del 2°tipo, la potenza del test è sempre 1-β

Un grafico costruito in modo da rappresentare i vari livelli di potenza, dati i vari valori alternativi della media, è chiamato curva di potenza.

Riprendendo il nostro esempio, con il valore alternativo alla media di 240.

β = P_{(errore seconda specie)} = 0.13
potenza = 1 – β = 1 – 0.13 = 0.87
Questa è la probabilità di rifiutare correttamente l’ipotesi nulla quando μ=240.

Determinare la dimensione che il campione deve avere per il test della media

Prima di prelevare un campione, posso determinare la dimensione che tale campione deve avere specificando:

1. Il valore ipotizzato della media
2. Il valore alternativo della media, tale che la sua differenza dal valore dell’ipotesi nulla sia considerato importante
3. Il livello di significatività del test
4. La probabilità ammessa di errore di tipo II
5. Scarto quadratico medio sigma della popolazione.

In formula:

\( n=\frac{(z_0-z_1)^2\sigma^2}{(\mu_1-\mu_0)^2}\\ \\ \)

Nell’esempio fisso come livelli accettabili

Errore I specie: 0.05
Errore II specie: 0.10
sigma=43

\( n=\frac{(z_0-z_1)^2\sigma^2}{(\mu_1-\mu_0)^2}=\\ \frac{(-1.65-1.28)^2(43)^2}{(240-260)^2}=\\ \frac{(8.5849 \cdot 1849)}{400}= 39.68 \approx 40 \\ \)

Il valore che stavo cercando è (circa) 40.

Al termine di tutto questo…E se non conosco i dati della popolazione?

Se non conosco il valore del sigma della popolazione, oppure se sto lavorando con piccoli campioni (meno di 30 valori) uso la distribuzione t o distribuzione di Student. Ma questo sarà l’oggetto di un prossimo articolo…