What is meant by a time series?
A time series consists of values observed over a set of sequentially ordered periods. This, for those who do SEO, is already an element of utmost interest.
Website traffic data, considered over a time sequence, is in fact an example of a time series.
Time series analysis is a set of methods that allow us to derive significant patterns or statistics from data with temporal information.
In very general terms, we can say that a time series is a sequence of random variables indexed in time.
The purpose of analyzing a time series can be descriptive (consider decomposing the series to remove seasonality elements or to highlight underlying trends) or inferential, with the latter including forecasting values for future time periods that have not yet occurred.
- What is meant by a time series?
- Creating a time series in R from a vector or data frame
- Plotting one or more time series
- Smoothing Techniques
- An Example of Using Time Series for SEO
- Exponential Smoothing with the Holt-Winters Method and Forecasting
- Investigating Time Series with ARIMA Models
- The ARIMA Model in Action
- Let's See a Practical Example of an ARIMA Model
- Time Series Analysis and Forecasting in R
A bit of theory. Classical time series analysis. Decomposing a time series.
The classical method of time series analysis identifies four influences, or components:
- Trend (T): the general long-term movement of the values (Y) of the time series over a long period of time.
- Cyclical Fluctuations (C): recurring long-duration movements.
- Seasonal Variations (S): fluctuations due to the particular time of year, for example the summer season compared to the winter months.
- Erratic or Irregular Movements (I): irregular deviations from the trend, which cannot be attributed to cyclical or seasonal influences.
According to the classical time series analysis model, the value of the variable in each period is determined by the influences of the four components.
The main purpose of classical time series analysis is precisely to decompose the series, to isolate the influences of the various components that determine the values of the time series.
The four “classical” components and their relationship
The four components can be related to each other additively:
Y = T + C + S + I
or multiplicatively:
Y = T x C x S x I
Recall that a multiplicative model can be transformed into an additive model by exploiting the properties of logarithms:
log(Y) = log(T) + log(C) + log(S) + log(I)
A brief review: the useful properties of logarithms
The logarithm of a number n to the base c (with c not equal to 1 and c > 0) is the exponent to which the base c must be raised to obtain n.
Therefore, if n = cb then logc n = b
- When numbers are multiplied together, the logarithm of their product is the sum of their logarithms.
- The logarithm of a fraction is the logarithm of the numerator minus the logarithm of the denominator.
- The logarithm of a number with an exponent is the logarithm multiplied by the exponent of the number.
Creating a time series in R from a vector or data frame
There are various ways to transform a data vector, a matrix, or a data frame into a time series.
Here, we will limit ourselves to the tools offered by base R to achieve this result.
The function of interest is simply called ts() and its use is rather intuitive.
Let’s see a practical example. Suppose we have a data vector saved with the name mydata.csv in the /home folder of my PC.
The first thing I will do is import my data into R, which I assume is in a CSV file:
# import the data from a csv file into a dataframe
dfmydata <- read_csv(“/home/mydata.csv”)
# create a vector with the data I'm interested in
mydata <- dfmydata$myobservation
Now all I have to do is call the ts() function with the appropriate start and frequency values to create my time series.
Let’s assume that the data is monthly, starting with January 2012 and going up to December 2018:
timeseries <- ts(mydata, start=c(2012,1), end=c(2018,12), frequency=12)
As you can see, the typical form of the ts() function is
ts(vector, start, end, frequency)
where frequency is the number of observations per unit of time.
Therefore, we will have 1=annual, 4=quarterly, 12=monthly…
Useful functions related to a time series
I can easily find out the time of the first observation of a time series using the command:
start()
Similarly, I can find the last observation with:
end()
The command:
frequency()
returns the number of observations per unit of time, while the very useful command
window()
allows you to extract a subset of data.
Using as an example a dataset included in R called Nile containing 100 annual readings of the Nile river at Aswan for the years 1871 to 1970 (we will also use it in the following paragraph), the command looks like this:
nile_sub <- window(Nile, start=1940,end=1960)
Plotting one or more time series
One of the advantages of using time series is the simplicity in graphical representation. Using the Nile example dataset present in R, which is already a time series object – and I can verify this with the command is.ts(Nile) – I just need the command:
plot.ts(Nile)
to get a graph of the trend of my variable over time. Obviously, I can use the various attributes xlab, ylab, main etc… to make my graph even more meaningful and clear:
plot(Nile, xlab="Year", ylab="Annual Nile River Flow", main="Example Time Series: Nile")
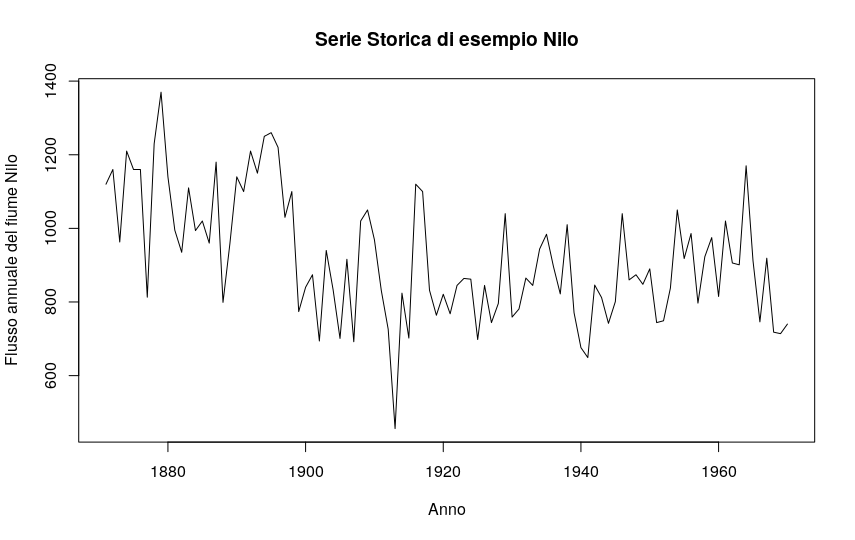
If the dataset contains more than one time series object, I can get the graph of the various objects.
Let’s use another example dataset present in R called EuStockMarkets which contains, as you can easily imagine, the prices of the FTSE, CAC, DAX and SMI stock markets:
plot(EuStockMarkets, plot.type = "multiple",)
If the dataset contains more than one time series object, I can obtain a graph of the various objects.
Let’s use another example dataset present in R called EuStockMarkets, which contains, as you can easily imagine, the prices of the FTSE, CAC, DAX, and SMI stock markets:
plot(EuStockMarkets, plot.type = "multiple",)
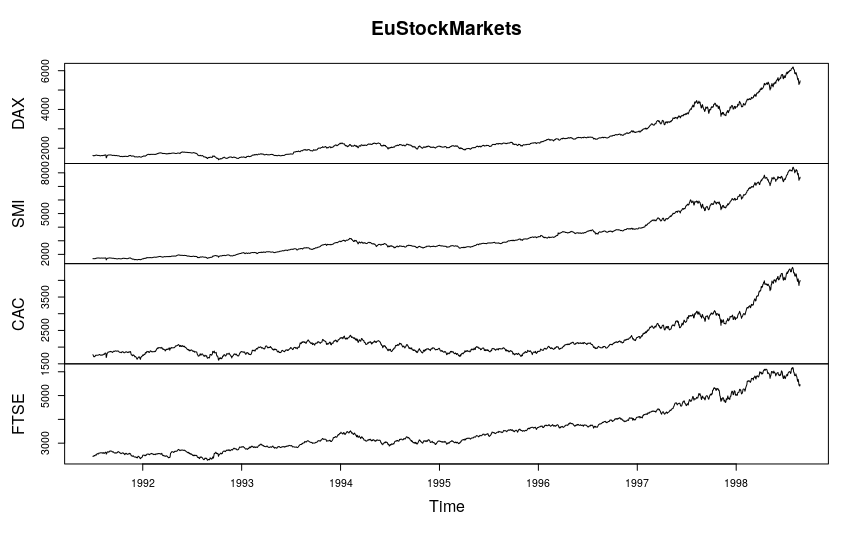
Alternatively, I can plot the various time series objects together—with different colors—in the same graph:
plot.ts(EuStockMarkets, plot.type = "single", col=c("red","black","blue","green"))
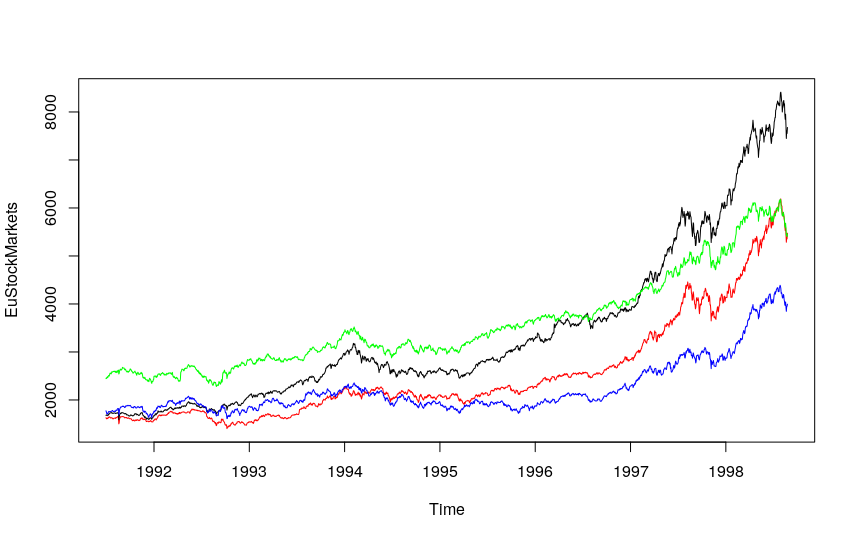
Smoothing Techniques
If we graphically represent a time series, we will almost always notice a series of small variations that can make it very difficult to identify important trends and make predictions for the future. To address this problem, various “smoothing” techniques have been developed, which we can, for simplicity, divide into two main families: techniques based on moving averages and exponential techniques.
MOVING AVERAGE
Instead of the data for month X, I calculate the average of n months, where X is the central point.
The random component is compensated for if we put several months together; its average is equal to 0 for a reasonable number of periods.
The seasonal component repeats regularly throughout the year, so if I distribute the seasonal effect over all 12 months, the effect disappears.
With the moving average, I achieve both desired effects: I compensate for randomness and “distribute” seasonality.
R, as we will soon see, provides fundamental help by making a whole series of tools available to us to carry out our analyses with maximum practicality.
An Example of Using Time Series for SEO
As we have seen, we can easily create a time series in R using the basic command ts().
Since I intend to use time series analysis for SEO purposes to derive a trend and make a forecast, I need to import data from my Google Analytics view into R.
I can do this “automatically” using the very useful googleAnalyticsR library (which may be the subject of a more detailed subsequent post) or by exporting the data I need via Query Explorer.
Let’s see the first case:
# use the googleAnalyticsR library
# which obviously I must have
# correctly installed
library(googleAnalyticsR)
# set the ID of my view
# numeric code ids that I find
# in Analytics or in Query Explorer:
view_id <- xxxxxxxxxx
# Authorize Google Analytics
ga_auth()
# Retrieve the data I need
# sessions from the beginning of 2017
# to the end of 2019 - from Google Analytics
gadata <- google_analytics(view_id,
date_range = c("2017-01-01", "2019-12-31"),
metrics = "sessions",
dimensions = c("yearMonth"),
max = -1)
# Convert the data into a time series
# with monthly frequency by indicating frequency=12:
ga_ts <- ts(gadata$sessions, start = c(2017,01), end = c(2019,12), frequency = 12)
The procedure to obtain the same result starting from a TSV file is just as simple.
First, I go to the Query Explorer interface
and select my account and view.
I choose the start and end dates (in my example, from January 1, 2017, to December 31, 2019), the metric I’m interested in (ga:sessions), and the dimension (ga:date).
One click on the “Run Query” button and I will have the result on the screen, which I can download locally by clicking on “Download Results as TSV”.
In my example, I save the file as filename.tsv
Now I open the file with a text editor and delete the first lines with the general information and the grand total at the bottom of the file.
If I want, I can rename the header row, replacing “ga:date” with “date” and “ga:sessions” with “sessions”, for better readability.
All that remains is to import the TSV and create the time series. A matter of two lines:
# Import a very simple dataset
# with date and users per day
sitomese <- read.csv('c:/path/filename.tsv', header = TRUE, sep = "\t")
# Convert the data into a time series
sitomese_ts <- ts(sitomese$sessioni, start = c(2017,01), end = c(2019,12), frequency = 12)
Now that I have my time series, I have a multitude of R packages available that provide me with all the useful tools for any type of analysis, from the most basic to the most in-depth.
Limiting the Effect of Seasonality Through Moving Averages
Install the forecast package to be able to use the very useful ma() function:
library(forecast) sitomese.filt <- ma(sitomese_ts, order=12) sitomese.filt
In this way, a weighted average has been applied to our time series to limit the effect of seasonality. I can now visualize the estimated trend using the moving average system:
lines(sitomese.filt, col="red")
Removing the Seasonal Trend Using Differencing
Using differencing with the diff() function and an appropriate lag, I can eliminate the seasonal trend, if present. In the case of a monthly time series that includes several years of observations, I just need to use a lag=12, as in this trivial example where I assume I’m working on a time series x:
# remove the seasonal trend # assuming monthly data and the presence of seasonality dx <- diff(x, lag=12) ts.plot(dx, main="Deseasonalized User Trend")
Decomposing the Time Series Through Moving Averages
We have seen in the course of the article that the classical method of time series analysis identifies four influences, or components, and that the main purpose is precisely to decompose the series to isolate the influences of the various components that determine the values of the time series.
Moving from theory to practice, let’s see how we can proceed.
I can use the decompose() function of the stats package to perform a classical decomposition of my time series into its components using the moving average system and representing everything in a single clear graph:
# decompose the time series. I have chosen a multiplicative decomposition # obviously, I could have chosen an additive one componenti <- decompose(sitomese_ts, type ="multiplicative") names(componenti) # explore the components of the time series in the graph plot(componenti)
Decomposing the Series with the LOESS Method
A more refined alternative for decomposing the series is the one that uses the LOESS (Locally Weighted Smoothing) method. It is a set of non-parametric methods that fit polynomial regression models to subsets of the data. We use the stl() function of the stats package for this purpose:
# use stl for a LOESS type decomposition sitomese_loess <- stl(sitomese_ts, s.window="periodic") names(sitomese_loess) plot(sitomese_loess)
Exponential Smoothing with the Holt-Winters Method and Forecasting
Smoothing and forecasting techniques offer us powerful operating modes for predicting future values of time series data.
At the most basic level, smoothing can be achieved using moving averages.
In R, we can use HoltWinters, a function to perform time series smoothing.
The function contains three exponential smoothing methods. All three methods use the same function, HoltWinters. However, we can invoke them separately based on the values of the alpha, beta, and gamma parameters.
Holt-Winters exponential smoothing provides reliable forecasts only if there is no autocorrelation in the time series data, which can be verified, as we will see shortly in practice, with the acf function and a Box-Pierce or Ljung-Box test.
After creating a forecasting model, we must evaluate it to understand if it correctly represents the data. Similar to a regression model, we can use residuals for this purpose. If the residuals follow a white noise distribution, then the sequence (or error) of residuals is generated by a stochastic process. And therefore, our model represents the time series well.
Let’s see an example. Suppose we have a time series x:
# We use the forecast function for a prediction: next 6 periods future.forecast <- forecast(x.forecast, h=6) # print a summary to the screen summary(future.forecast) # draw the graph plot(future.forecast) # draw the graph of the residuals to estimate the autocorrelation acf(future.forecast$residuals, na.action = na.pass) # perform an autocorrelation test Box.test(future.forecast$residuals)
Autocorrelation tells us whether the terms of a time series depend on its past.
If we consider a time series x of length n, the lag 1 autocorrelation can be estimated as the correlation of the pair of observations (x[t], x[t-1]).
R provides us with a convenient command: acf().
Using:
acf(x, lag.max = 1, plot = FALSE)
on the x series, the autocorrelation of degree -1 is automatically calculated.
By default, the command acf(x) draws a graph that shows two dashed blue horizontal lines, which represent the 95% confidence interval.
The autocorrelation estimate is indicated by the height of the vertical bars (obviously, the autocorrelation at degree 0 is always 1).
The confidence interval is used to determine the statistical significance of the autocorrelation.
I show, as an example, the output of the acf() function on the Nile time series provided by R:
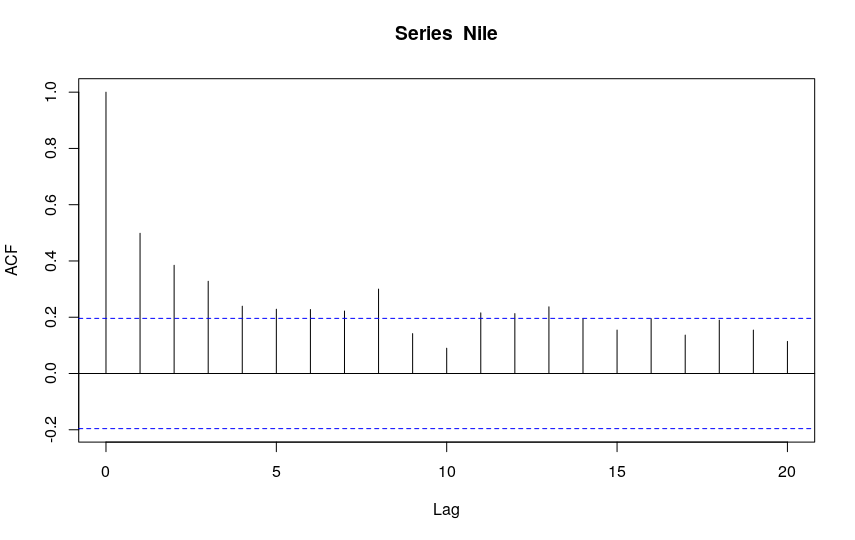
If the autocorrelation coefficient decreases and falls rapidly between the bounds, this means that the residuals follow a white noise distribution. There is no apparent autocorrelation.
Conversely, if the coefficients are always above or below the limit, this means that the residuals are autocorrelated.
A Ljung-Box autocorrelation test is a particular form of hypothesis test, and it provides a p-value as output, a value that allows us to understand whether to reject the null hypothesis or not.
Let’s apply the box.test function to the residual sequence; we find the p-value. If it is greater than the value of α, we cannot reject the null hypothesis. That is, the residuals are white noise, and this demonstrates that our model “works well” in predicting the value.
Let’s see it all in action in our SEO example related to website traffic, also using the highcharter library for better visualization of the output:
# First, I load the libraries I need
library(googleAnalyticsR)
# to read Analytics data
library(forecast)
# for time series forecasting
library(highcharter)
# to get the chart
# Here I insert the ID code
# to find it, just log in
# to Analytics Query Explorer
# https://ga-dev-tools.appspot.com/query-explorer/
# and read the "ids" value
# for the view we are interested in
view_id <- xxxxxxxxx
# Authorize Google Analytics
ga_auth()
# and then retrieve the data from Google Analytics
sitomese <- google_analytics_4(view_id,
date_range = c("2017-01-01", "2019-12-31"),
metrics = "sessions",
dimensions = c("yearMonth"),
max = -1)
# nb: the dimension of my data is yearMonth
# Now I express the data as a time series
sitomese_ts <- ts(sitomese$sessions, start = c(2017,01), end = c(2019,12), frequency = 12)
# Calculate Holt-Winters smoothing
previsione <- HoltWinters(sitomese_ts)
# Generate a forecast for the next 12 months
hchart(forecast(previsione, h = 12))
The reader is tasked with testing the quality of the forecasting model.
Investigating Time Series with ARIMA Models
Using the exponential smoothing method requires that the residuals are not correlated. In real-world cases, this is quite unlikely. However, we have other tools available to address these cases: R provides us with the ARIMA function to build time series models that take autocorrelation into account.
White Noise
The very useful arima.sim function allows you to simulate an ARIMA process by generating ad hoc time series data.
Through this function, therefore, we can begin to look at two basic time series models: white noise and the random walk.
An ARIMA model consists of three components: ARIMA(p,d,q).
- p is the order of autoregression
- d is the order of integration
- q is the order of the moving average
White noise is the most basic example of a stationary process. Its salient characteristics are:
- It has a fixed, constant mean.
- It has constant variance.
- It does not follow any temporal correlation.
The white noise model in ARIMA terms is therefore ARIMA(0,0,0).
Let’s simulate a time series of this type:
wn <- arima.sim(model = list(order = c(0,0,0)), n=100) ts.plot(wn)
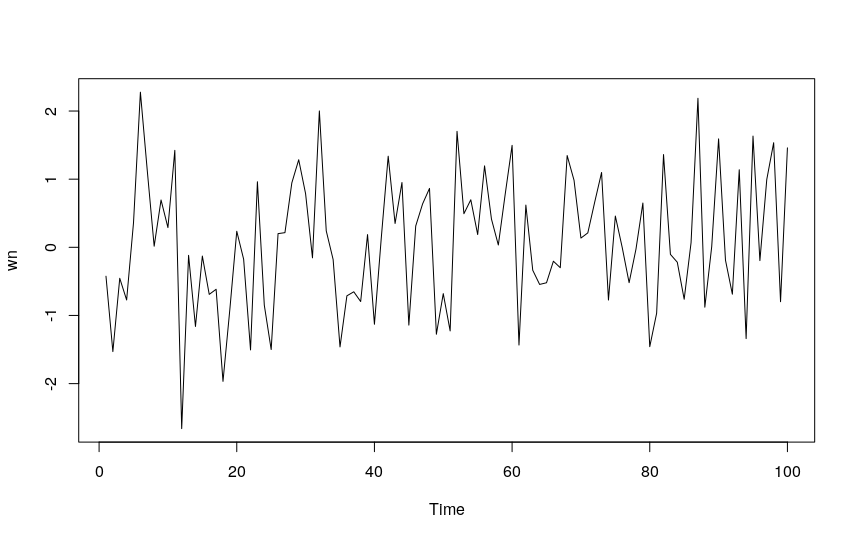
Random Walk
The Random Walk is a simple example of a non-stationary process. It has the following salient characteristics:
- It does not have a specific mean or variance.
- It shows strong temporal dependence.
- Its changes or increments are of the White Noise type.
The random walk model is also a basic time series model and can be easily simulated with our arima.sim function.
The Random Walk model is the cumulative sum of White Noise series with a mean of zero.
From this, it follows that the first differenced series of a Random Walk series is a White Noise series!
The ARIMA model for a Random Walk series is ARIMA(0,1,0).
Let’s generate a series of this type and visualize it:
RW <- arima.sim(model = list(order = c(0,1,0)), n = 100) ts.plot(RW)
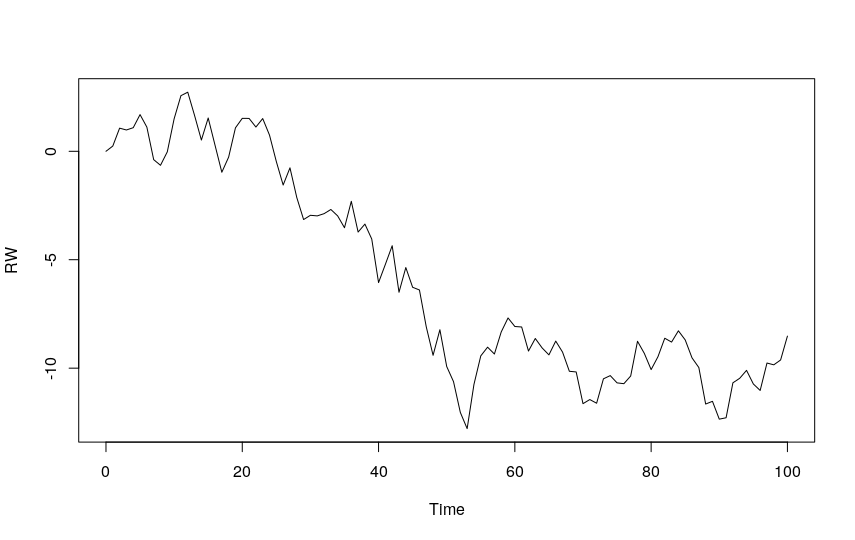
Let’s see the proof of what was stated above:
RWdiff <- diff(RW) ts.plot(RWdiff)
We obtain precisely a White Noise series:
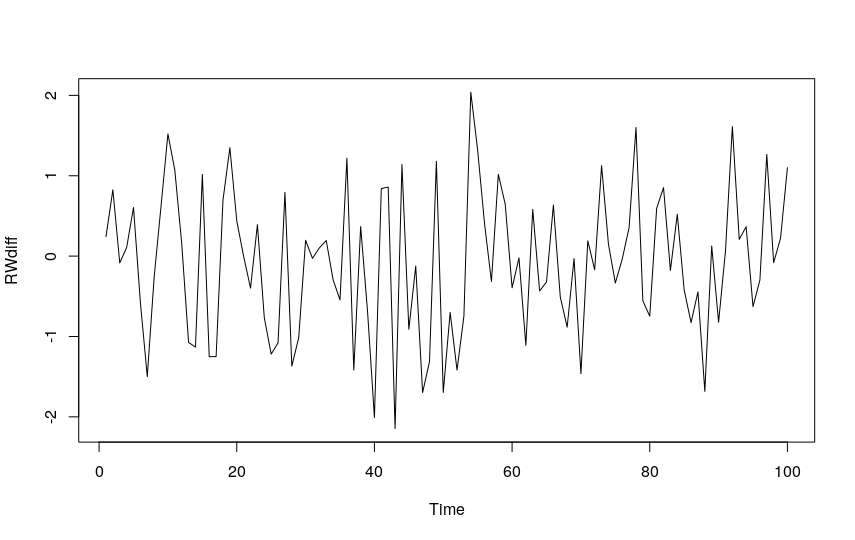
The ARIMA Model in Action
The Autoregressive Integrated Moving Average (ARIMA) model is also known as the Box-Jenkins model, named after statisticians George Box and Gwilym Jenkins.
The purpose of ARIMA is to find the model that best represents the values of a time series.
An ARIMA model can be expressed as ARIMA(p, d, q), where, as we have already seen, p is the order of the autoregressive model, d indicates the degree of differencing, and q indicates the order of the moving average.
Operationally, we can define five steps to fit time series to an ARIMA model:
- Visualize the time series with a graph.
- Difference non-stationary time series to obtain stationary time series.
- Plot ACF and PACF graphs to find the optimal values of p and q, or derive them using the
auto.arimafunction. - Build the ARIMA model.
- Make the forecast.
Let’s See a Practical Example of an ARIMA Model
1. Simulate an ARIMA process using the arima.sim() function and plot the graph:
simts <- arima.sim(list(order = c(1,1,0), ar = 0.64), n = 100) plot(simts)
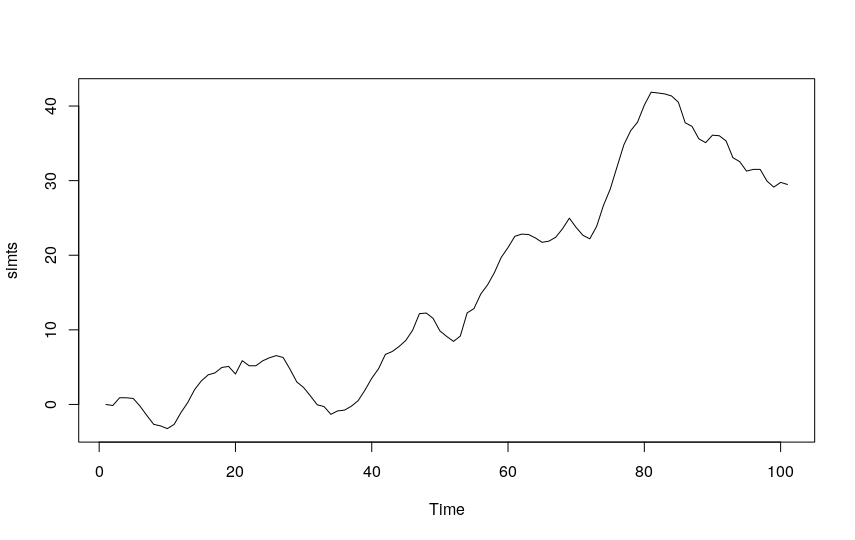
2. Difference the series to obtain a stationary time series and plot the graph:
simts.diff <- diff(simts) plot(simts.diff)
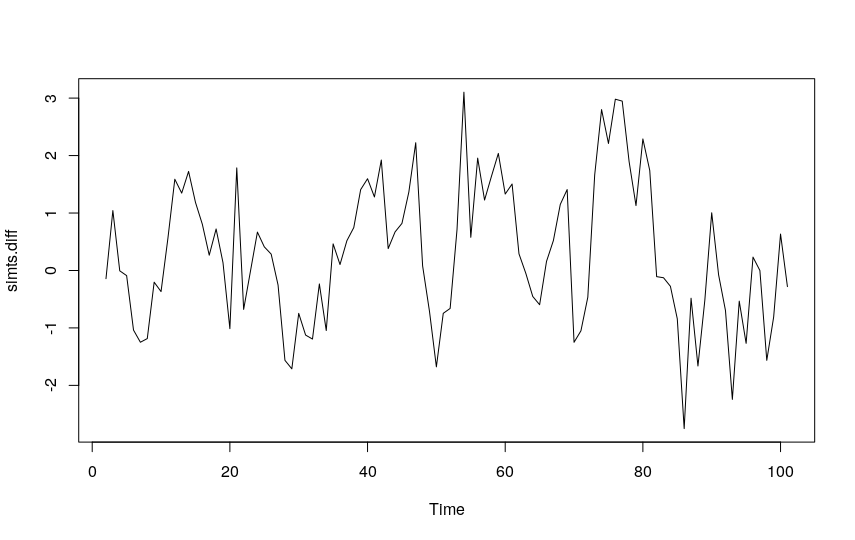
3. Use the auto.arima function to estimate the best values for p, d, and q:
auto.arima(simts, ic="bic") Series: simts ARIMA(1,1,0) Coefficients: ar1 0.6331 s.e. 0.0760 sigma^2 estimated as 0.9433: log likelihood=-138.73 AIC=281.46 AICc=281.58 BIC=286.67
4. Create the ARIMA model with the indicated p, d, and q values (in our example, 1, 1, 0):
fit <- Arima(simts, order=c(1,1,0)) summary(fit)
5. Based on our ARIMA model, we can now proceed to forecast future values of the series and plot the graph:
fit.forecast <- forecast(fit) # Changed fit.prev to fit.forecast for consistency summary(fit.forecast) plot(fit.forecast)
Time Series Analysis and Forecasting in R
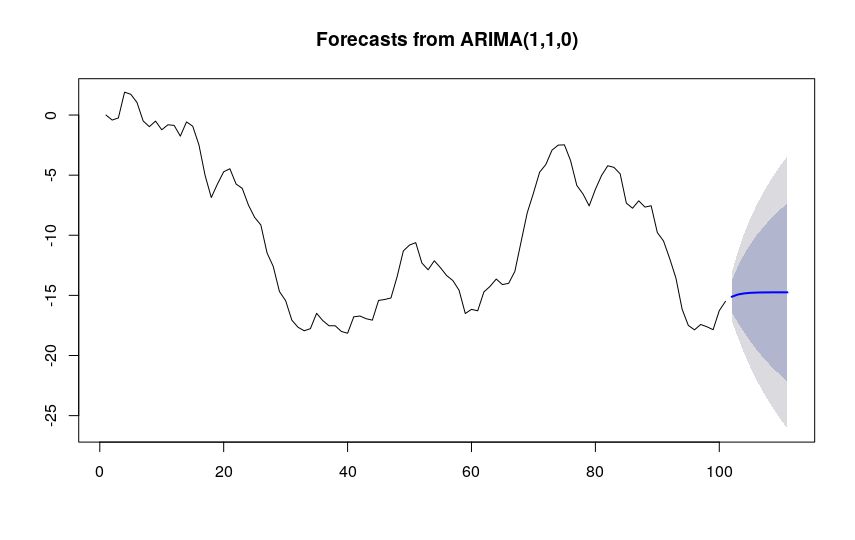
The shaded areas show the 80% and 95% confidence intervals.
Finally, let’s evaluate the goodness of our model with an ACF graph:
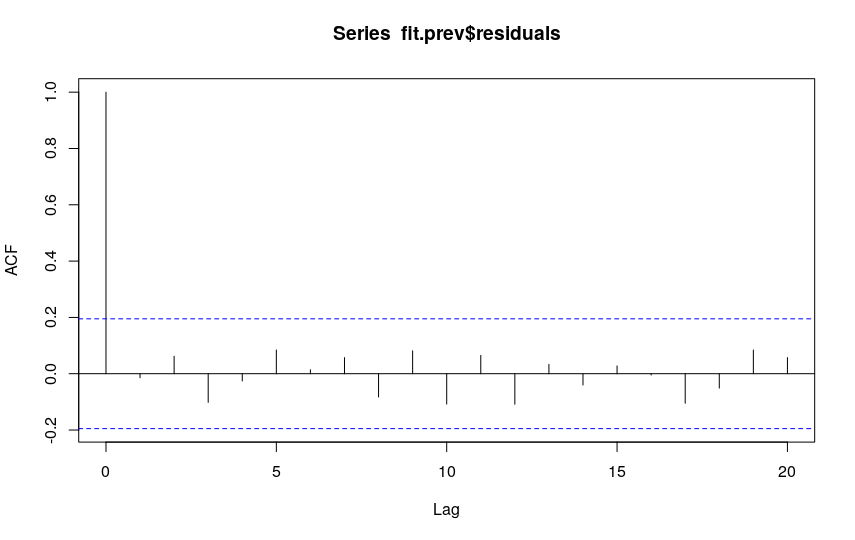
As with the exponential smoothing model, we can use the acf function to calculate the residuals and create the autocorrelation plot. Since the autocorrelation coefficient decreases rapidly, the residuals are white noise.
We can also perform a Box-Pierce test:
Box.test(fit.forecast$residuals) # Changed fit.prev to fit.forecast Box-Pierce test data: fit.forecast$residuals X-squared = 0.020633, df = 1, p-value = 0.8858
And we obtain a p-value that indicates the non-rejection of the null hypothesis.
